
自分でやるクレジットカード現金化の方法については、大きく分けると3つの方法があります。
-
商品券など金券ショップを使う
商品券を購入し金券ショップで売却。換金率が安定して高い。 -
ゲーム機・家電を転売
人気のゲーム機や家電も換金率が高いのでおすすめ。場合によっては換金率100%超えも! -
電子ギフト券を買い取ってもらう
Amazonギフト券やAppleギフトカードなど。換金率が高いのでおすすめ。
主に上記の3つです。
クレジットカード現金化の優良店を使わず自分で行う場合の各種メリット・デメリットなども解説しています。
| 1位 | 2位 | 3位 |
|---|---|---|
 |
 |
 |
| タイムリー | スピードペイ | プライムウォレット |
| https://cardtimely.com/ | https://speed-pays.com/ | https://prime-wallet.com/ |
| 来店・審査不要 | 年中無休 | LINEで見積もり可 |
|
最大換金率 98.6% |
最大換金率 98% |
最大換金率 98.8% |
| 最短3分 | 最短10分 | 最短10分 |
| 公式サイト | 公式サイト | 公式サイト |
目次
- 自分で行うクレジットカード現金化と業者を使うクレジットカード現金化の違い
-
自分でクレジットカード現金化をする方法14選
- クレジットカード現金化で業者を使わない方法1:ブランド品
- クレジットカード現金化で業者を使わない方法2:ゲーム機・ゲームソフト
- クレジットカード現金化で業者を使わない方法3:家電製品
- クレジットカード現金化で業者を使わない方法4:新幹線回数券
- クレジットカード現金化で業者を使わない方法5:商品券
- クレジットカード現金化で業者を使わない方法6:電子ギフト券で現金化する
- クレジットカード現金化で業者を使わない方法7:切手・はがき・レターパック
- クレジットカード現金化で業者を使わない方法8:電子マネー
- クレジットカード現金化で業者を使わない方法9:SuicaやPASMOなど交通系電子マネー
- クレジットカード現金化で業者を使わない方法10:QUOカード
- クレジットカード現金化で業者を使わない方法11:仮想通貨
- クレジットカード現金化で業者を使わない方法12:支払いの立て替え
- クレジットカード現金化で業者を使わない方法13:商品返品
- クレジットカード現金化で業者を使わない方法14:フリマアプリ・オークションを利用する
- クレジットカード現金化のとは?何のために利用するの?
- クレジットカード現金化のメリット・デメリット
- 自分でクレジットカード現金化をした方にアンケートをしました
- 業者を使わないで自分でクレジットカード現金化する流れ
- 業者を使わずに自分でクレジットカード現金化する時のメリット
- 業者を使わないで自分でクレジットカード現金化する時のデメリット
- 自分でクレジットカード現金化するときのよくある質問
- 自分でクレジットカード現金化はできるけれど 安全かつ多額の取引には優良業者の利用がおすすめ
自分で行うクレジットカード現金化と業者を使うクレジットカード現金化の違い
クレジットカード現金化を自分でやる場合と、業者を使う場合の違いを比較してみましょう。
| 自分で行う現金化 | 業者を使う現金化 | |
|---|---|---|
| 手軽さ |
商品選定、購入、売却と手間がかかる。 |
業者に一括して任せられる。 オンラインで完結する。 |
| 発覚するリスク |
カード会社に発覚しやすい。 |
優良業者ならトラブル0。 |
| 換金率 |
相場は70~90% レア商品などを売れば90%以上も可能。 |
相場は70~80% 手数料がかかる分、換金率は低くなる。 |
自分でクレジットカード現金化をする方法14選
クレジットカード現金化では、クレジットカードで購入ができ、換金性が高い、つまり、なるべく購入価格に近い金額で売れる商品を探すことが重要な裏ワザです。
換金性が高い商品には、さまざまなものがあります。
たとえば電化製品やブランド品、人気のゲーム機、ゲームソフトなどは、換金性が高い商品として有名です。
これらは定価の80%〜95%で売却できるため、これらの換金性の高い商品を使って自分で現金化すれば、低い換金率の現金化業者を使うよりも好条件で現金化できます。
自分でクレジットカード現金化を行う場合に使える商品や方法を紹介します。
クレジットカード現金化で業者を使わない方法1:ブランド品
ブランド品の中でも、
- エルメス
- ロレックス
- ルイ・ヴィトン
といった誰もが知っている人気ブランドの商品を転売すれば、簡単に高換金率を狙うことができます。
ただし、知名度が低く不人気のブランド品や、人気ブランドでも既にデザインが古くなり人気がなくなったタイプを選んでしまうと、業者に買い叩かれて50%以下の換金率になってしまうことがあるので注意してください。
あまり手間をかけたくない、リスクは最小限にしたいと考える方には、積極的におすすめできる方法ではありません。
クレジットカード現金化で業者を使わない方法2:ゲーム機・ゲームソフト
人気のゲーム機や新作ゲームソフトは価格が手頃で誰でも簡単に購入できるので、少額の現金化を行うのに手軽でおすすめの商品です。
ゲーム機やゲームソフトは買取り相場の変動が激しいですが、商品の選択と売るタイミングが良ければ70%前後の高換金率を狙えます。
特にゲーム機は需要が高まると定価以上の値段で売れることがあるので、話題のゲーム機は早めにゲットしておきましょう。
ゲーム機なら4~5万円以内、ゲームソフトなら1~2万円以内の商品にして、少額の現金化に留めておくのが安全です。
クレジットカード現金化で業者を使わない方法3:家電製品
スマホやパソコン、テレビといった家電製品はクレジットカードで購入してもカード会社に怪しまれにくいため、現金化に向いている商品です。
ただし、テレビや冷蔵庫のような大型家電は購入後に換金する際、店舗への持ち込み、あるいは梱包・発送作業が手間になるため、ノートパソコンやデジカメ、スマホなどの小型家電がおすすめです。
特に、スマホの人気ブランド(iPhoneやGalaxyなど)の最新機種は常に買取価格が高額なのでおすすめです。
家電量販店のセールを利用したり、値引き交渉を行ったりして商品を安く購入できれば、100%以上の換金率になることがあります。
クレジットカード現金化で業者を使わない方法4:新幹線回数券
新幹線回数券は90%以上の高い換金率で売れることから非常に人気があり、昔から現金化の定番として重宝されてきました。
特に、東京から大阪・名古屋・京都などへ向かう人気区間の回数券は、95%~98%の高換金率で売れることから、人気区間の回数券を1冊(6枚綴り)転売するだけで一度に5~6万円の現金化が可能でした。
しかし、JR側もネット予約サービスの整備とともに、新幹線回数券を徐々に廃止しており、今後新幹線回数券を使った現金化は難しくなるものと思われます。
| JR東日本 | 完全廃止 |
|---|---|
| JR東海 | ほぼ廃止(普通車自由席の一部区間は販売継続) |
| JR西日本 | 完全廃止 |
また、もし手元に使用予定のない新幹線回数券が残っているなら、早めの換金をおすすめします。
クレジットカード現金化で業者を使わない方法5:商品券
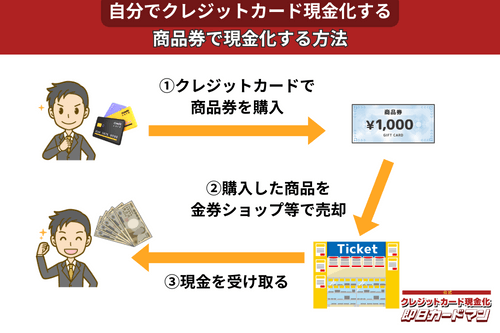
金券ショップで高い換金率で現金化できるのが、百貨店やクレジットカード会社が発行する商品券です。
商品券は特段の目利き力を必要せず、持ち運びが簡単であり、かつ即日現金化ができることもメリットと言えます。
商品券を簡単に高く売る方法は、駅前や街中にある金券ショップに直接持ち込むことです。
商品券をネットの個人間取引で売る方法もありますが、多くのフリマアプリやオークションでは商品券の出品が禁止されています。
商品券の出品が可能な場合でも、高額な手数料が発生して換金率が10%ほど下がってしまうので注意が必要です。
クレジットカード現金化で業者を使わない方法6:電子ギフト券で現金化する
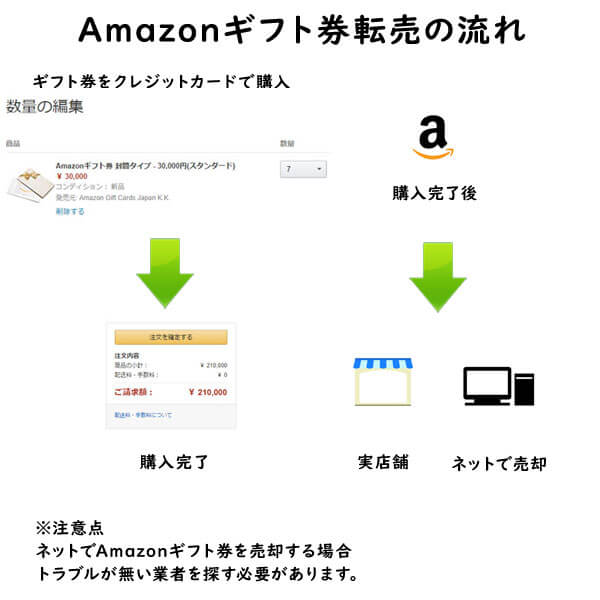
最近、注目されているクレジットカード現金化の裏ワザがAmazonギフト券などの電子ギフト券です。
電子ギフト券はインターネットの通販サイトで主に使えるもので、電子ギフト券に付与されたギフト券番号で支払いを行います。
ギフト券購入もネットで行えることから、支払いもクレジットカードが利用できるものが多いのです。
この性質を利用して、電子ギフト券をネットで買取りする業者が増えており、ネットでギフト券を購入してネットの現金化業者を利用すれば、家に居ながらにして商品購入から現金化まで行えます。
ただし、クレジットカード会社に加え、Amazonなどギフト券を発行する発行会社もギフト券を使った現金化を利用規約で禁止しているので、繰り返しギフト券を購入するなど目立った購入履歴があるとペナルティが課されますので注意しましょう。
また、電子ギフト券はギフト券番号をその通販サイトの自分のアカウントに登録しないと未使用か、使用期限がいつまでか確認できません。しかし、一度登録してしまうと他の人に譲渡できなくなります。
こうした電子ギフト券の特徴から街中の金券ショップでは電子ギフト券の取り扱いを中止しているところが多いため、電子ギフト券の売却はネットの買取業者を利用することをおすすめします。
電子ギフト券の現金化方法やその注意点については、関連ページでくわしく紹介していますので、参考にしてください。
関連ページ:Amazonギフト券買取おすすめ優良業者ランキング【アマゾンくん】
クレジットカード現金化で業者を使わない方法7:切手・はがき・レターパック
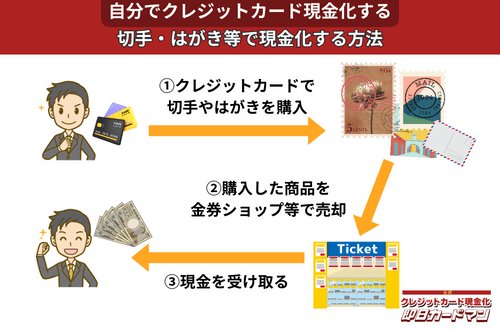
キャッシュレス決済対応の郵便局であれば、クレジットカード、電子マネー、スマホ決済が利用できます。クレジットカードで切手やはがき、レターパックを購入して、金券ショップに売却すればすぐに現金を手に入れることができます。
ただし、郵便局では切手販売に限り1回の取引は10万円が上限額となります。
また簡易郵便局の場合、切手、はがき、レターパックの店頭販売は3万円が上限額となり、クレジットカードと電子マネーの利用はできません。
クレジットカード現金化で業者を使わない方法8:電子マネー
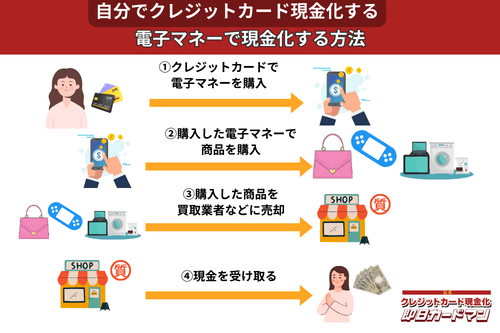
2019年からのキャッシュレス推進政策によって普及に弾みがついた電子マネー(nanaco、楽天Edy、WAON、交通系電子マネーなど)は、クレジットカード現金化にも使えます。
電子マネーの現金化はクレジットカード会社に気づかれにくく、しかも商品の転売に伴う手間(店舗への持ち込みや梱包・発送作業)が不要なので手軽に現金化できます。
電子マネーの現金化と聞くとややこしそうに思えるかもしれませんが、誰でも簡単に現金化が可能です。
下記のページで詳細を解説しています。
クレジットカード現金化で業者を使わない方法9:SuicaやPASMOなど交通系電子マネー
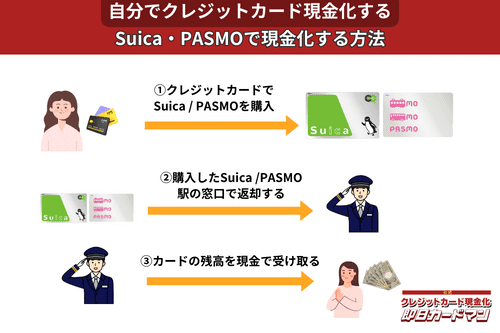
SuicaやPASMOなどの交通系電子マネーに関しては、チャージを行った駅の窓口で払い戻しが可能です。
その際、払い戻し手続きに必要な身分証明書(運転免許証やパスポートなど)を忘れずに持参しましょう。
ただし、チャージした駅と異なる駅の窓口で払い戻しを行ったり、払い戻しを行う日がチャージ日の翌日以降になったりすると、払い戻し手数料(1回につき220円)が発生してしまうので注意してください。
また、アプリ型の電子マネー「モバイルSuica」は返金に数週間以上要することがあるので、即日現金化には向いていません。
クレジットカード現金化で業者を使わない方法10:QUOカード
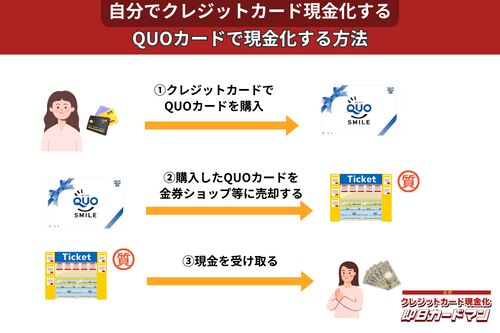
クレジットカードでの購入が難しくなっているプリペイドカードですが、一部のQUOカードはクレジットカードでの購入が可能です。
クレジットカードで購入する方法としては、
- クオカードオンラインストアで買う。
- JCB-QUOカードをJCBカードで買う。
- ファミリーマートで、クレジットカード機能付きファミマTカードで買う。
- セブンイレブンで、クレジットチャージしたnanacoで買う。
という4つの方法が知られています。
いずれも、購入後、金券ショップで売却すれば、すぐに現金化できます。
ただし、オンラインでの購入には発送手数料がかかりますので、その分換金率が下がります。
クレジットカード現金化を目的とする場合は、できるだけ高額をまとめて買うことが裏ワザになります。
クレジットカード現金化で業者を使わない方法11:仮想通貨
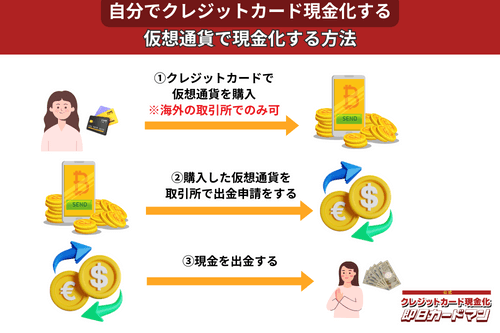
2017年頃から一躍ブームとなった「ビットコイン」や「イーサリアム」など、仮想通貨を使った方法も一応現金化は可能ですが、手順が複雑なので初心者向きではありません。
以前はクレジットカードで簡単に仮想通貨を購入できたので現金化も容易でしたが、現在は仮想通貨の購入方法に規制がかけられているので、国内取引所ではクレジットカードが使えなくなっています。
このため、仮想通貨でクレジットカード現金化を行うには、規制が緩くクレジットカード決済が可能な海外サービス(取引所または両替所)を利用するしかありません。
クレジットカード現金化で業者を使わない方法12:支払いの立て替え
友人や会社の同僚との食事会や飲み会の際、集金担当になり会費を現金で徴収して支払いをクレジットカードにすれば、現金を手に入れることができ、クレジットカード現金化になります。
ただし、ほかに集金係が現れたら現金化できません。また、飲食代の立て替えは人数が多いほど換金率が高くなり、反対に2人だけの場合は換金率50%になってしまいます。
クレジットカード現金化で業者を使わない方法13:商品返品

クレジットカードで購入した商品を返品して、現金で返金してもらえば、クレジットカード現金化になります。
ただし、ネット通販で購入した場合、返金額は次のクレジットカード払いから相殺される場合が多く、現金を手に入れることはできません。
店舗での購入の場合、現金で返金される場合がありますが、これも店舗により事情が異なります。
というのも、店側も対策を講じてカードで購入した商品の返品時の返金はカードで処理し、次回、あるいは次々回のクレジットカード支払金額から返金額をマイナスする形で処理するようにしているためです。
購入と返品を繰り返すことで、店側から利用停止・退会処分のペナルティを課されてしまう可能性もあるため、安全かつ確実に現金化したいのであれば他の方法をおすすめします。
クレジットカード現金化で業者を使わない方法14:フリマアプリ・オークションを利用する

買取業者では現金化が難しい、あるいは換金率が低い商品は、フリマアプリやネットオークションを利用してみるのもひとつの方法です。
一方で、個人間の取引はトラブルが発生しやすく、また落札されないリスクがあるので、急いで現金化したい方にはおすすめできません。
オークションやフリマアプリで売却するなら、定価以上の価格でも買いたいと思われるような人気商品(洋服やアイドルグッズ、おもちゃなど)を選ぶのがおすすめです。
ただし、商品によっては出品できないもの(チケット・金券類や正規品の確証がないブランド品など)があるので確認が必要です。
また、こうした取引では出品・落札手数料や送料、梱包資材の費用、銀行への振込手数料といった諸々のコストも考慮に入れておく必要があります。

以上、14のクレジットカード現金化の方法を紹介しました。
クレジットカード現金化のとは?何のために利用するの?

そもそもクレジットカードの現金化とは、ショッピング枠で商品を購入し、業者からキャッシュバックなどで現金を得ることを指します。
クレジットカードには、商品やサービスを購入し、後払いにする「ショッピング」の機能と、お金を借り入れる「キャッシング」の機能があり、それぞれに利用できる金額が設定されています。
「クレジットカードショッピング枠の現金化」とは、本来、商品やサービスを後払いするために設定されている「ショッピング」の利用可能枠を換金する目的で利用することです。
引用:一般社団法人日本クレジット協会
クレジットカード現金化の仕組みについても知っておきましょう。
自分で現金化をする場合でも、基本的に同じ仕組みです。
では、そのクレジットカードの現金化をする人は、何のためにするのでしょうか?
それは、現金が手元になく、いますぐ必要な方にとってはとても便利な方法なので利用されています。
現金を手に入れる方法は他にもありますが、キャッシング枠を使い切っている人で即日必要な場合など重宝します。
特にフリーローンや消費者金融など、審査が必要な方法では待てないという方にとっては利点です。
関連ページ:クレジットカード現金化の目的は何のため?メリットと特徴を知って無職・低年収でもできる
クレジットカード現金化のメリット・デメリット
クレジットカード現金化のメリットとデメリットを紹介します。
| 現金化 | メリット | デメリット |
|---|---|---|
| 利用できる人 | 20歳以上で自分名義の クレジットカードがあれば利用できる |
ショッピング枠の限度額までしか利用できない。 |
| 審査 | 借金ではないので審査を受ける必要はない | 実際は借金と同じで返済しなければならない |
| ペナルティ | 信用情報機関に借金履歴かとして残らない | カード会社に発覚したら 利用停止、退会処分、一括返済など 重いペナルティが科せられる |
| 利息・手数料 | 借金ではないので利息がかからない | 手数料がかかる |
| 利用時間 | 24時間365日いつでも利用できる | 中には申し込みのみ24時間受付という業者もある |
| 安全性 | 優良業者を選べば安全に利用できる | 悪質業者が混ざっているので 業者選びが重要である |
| 入金までのスピード | 即日入金が可能である | 自分の銀行口座は 24時間入出金可能か確認が必要である |
クレジットカード現金化は、既に多額の借り入れがあり、消費者金融などでは審査に通らない人でも、ショッピング枠に余裕があるクレジットカードがあれば、審査なしで現金をすぐに入手できる便利な方法といえます。
ただし、カード会社に現金化していることを知られてしまうと、カード利用停止や退会処分などのペナルティが科せられるリスクがあるため、利用頻度などに注意が必要です。
また、審査がなく買い物感覚で利用できるからと多額の現金化をしてしまうと、返済が滞り多重債務に陥ってしまう危険があります。
利用額は返せる範囲に留めて利用することが大切です。
自分でクレジットカード現金化をした方にアンケートをしました
当サイトではクラウドソーシングサービスを使って、実際に自分でクレジットカード現金化をした方を対象にアンケート調査を行いました。
有効回答数は19件と少ないですが、経験した方の感想などを紹介します。
現金化した人の年齢・性別
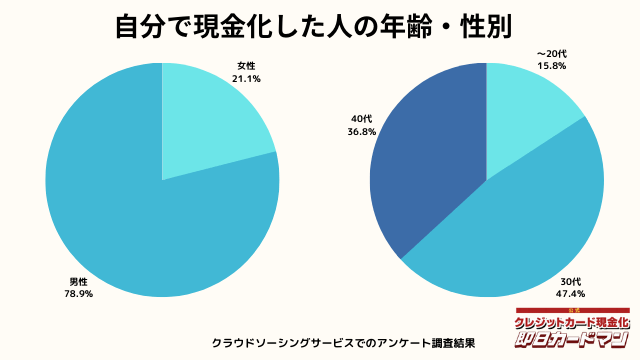
年齢と性別ですが、30代・男性が最も多い利用者でした。
急用で現金が必要になるシーンは、若い方よりも30代~40代の世代が多いようです。
女性の方も少ないですが、数人の方が利用していました。
いくら現金化できましたか?
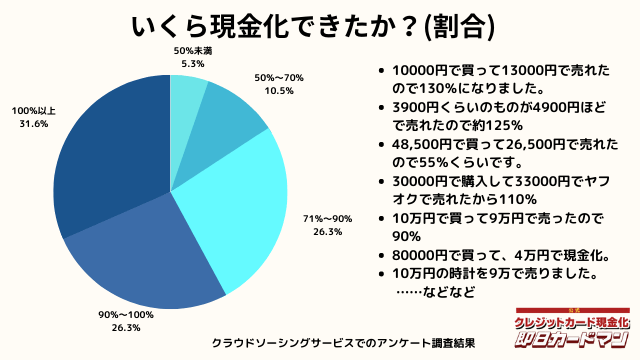
気になる換金率についても調査しました。
おおよそ70%~90%台が多く、中には100%以上の換金率を実現した方もいます。
業者に依頼するとこのような換金率にはならないので、個人で行う最大のメリットが現れた形です。
ですが、70%以下になる場合もあります。今回のアンケートで最も低かったのが50%の方です。
現金化するまでにかかった時間
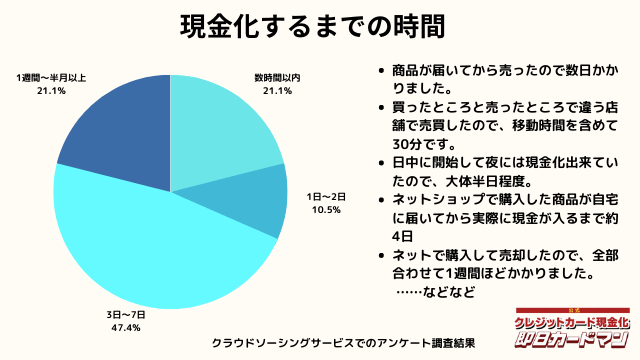
現金化するまでにかかった時間についてもまとめました。
これは商品の購入~実際に現金を手にするまでの時間を回答して頂きました。
自分で現金化する場合、購入~売却まで全ての作業を行わなければいけません。
手間暇・労力をかけるに値するか、多少換金率が下がったとしても業者に依頼するかは慎重に検討しましょう。
その他の回答として下記があります。
商品購入してから売却するまでに1周囲間程度かかり、手元に現金が入ったのがその3日後なので、全部で10日240時間かかりました。
半日ほどで売れて取引完了までに3日くらいかかった
約5日間かかりました。
自分で現金化したときの方法や商品
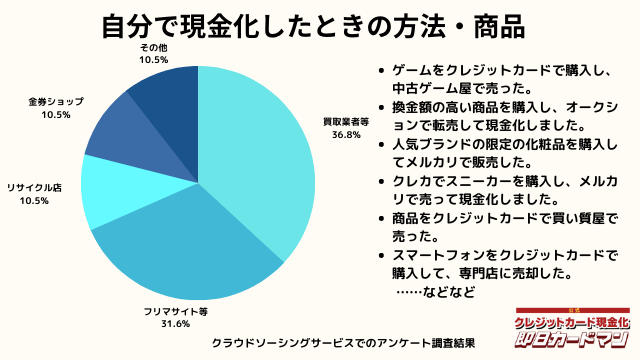
自分で現金化したときの方法としては、専門店や買取業者などに売却する方が最も多いようです。
メルカリ・ヤフオクなどを使ったフリマサイトも同程度あります。
ギフトカードを購入し、金券ショップで売却した方もいらっしゃいました。
その他の意見として、下記の回答もありました。
店舗で商品券を買って、金券ショップで売却しました。
ポケモンカードをヤフオクで落札して転売しました
急いで現金が欲しかったので先月高級ブランド品を売っている高島屋のルイ・ヴィトンの正規店で財布をクレジットカードで購入して、それを買取業者ですぐに売却しました。
カード会社からの警告やトラブルについて

カード会社にバレたりしたのか、警告があったのか回答して頂きました。
今回のアンケートでは全員カード会社にバレていないという結果になりました。
またバレないようにしている工夫なども回答して頂いております。
明らかな転売目的と分かるような高額な買い物はしないようにしています。また、頻度を抑えて週に1回程度にすることでいまだにバレたことはないです。
バレそうな時の言い訳を考えておく。間違えて購入してしまい不要になった、など。
高額商品をクレジットカードで購入することはありますが、一度購入したらその次は日用品や食料品などをクレジットカードして、さらに数か月経ってからクレジットカードのショッピング枠を現金化するように対策をしています。
普段使いでもしっかり利用するようにしている。
業者に依頼しなかった理由について
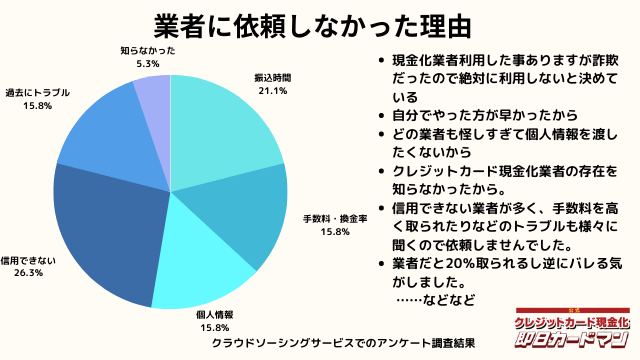
最後に自分でクレジットカード現金化を行わず、業者に依頼しなかった理由について紹介します。
回答した方によって理由は様々でした。
振込までの時間を考慮した、自分でやる方が早い、業者は信用できそうにない、換金率・手数料についての不満、個人情報を渡すのが怖い、というのが主な理由です。
中にはトラブルに遭った方もおりました。具体的なエピソードも交えて紹介します。
知識の豊富な友人がいたので、業者に頼って手数料を支払わなくても済む友人に頼って実行したため、最初から依頼することは考えていませんでした。
クレジットカード現金化業者を利用することも確かにありますが、前に利用したクレジットカード現金化業者の対応が悪質で換金率が大幅に減らされたことで頭にきたこともあって、今回は高級ブランド品をクレジットカードで購入してそれを売却して現金化しようと考えたからです。
業界団体に未加入の業者がトラブルの元だから。
すぐ手元に元気が欲しかった。もし、業者で依頼し換金率が高ければ、依頼してたかもしれない。
前々からせどりをしてたので垢が育ってたのと販売から発送までの手順は熟知しているのでわざわざ業者に頼む必要がなかった。住所を教えれば送り付け商法等の詐欺被害に会いかねないので教えたくなかった。それとクレジットカードの不正利用をされたくなかったので業者は利用しなかった。
業者を利用すると手数料や換金率など売却するのに費用がかかってくるので、なるべくお金を手元に残したいため、業者に依頼しませんでした。
業者を使わないで自分でクレジットカード現金化する流れ

自分でクレジットカード現金化を行う方法は、そんなに難しいものではありません。
現金化に利用するアイテムによって、購入方法や売却方法は変わりますが、基本的な方法、現金化の流れは同じです。
実際に業者を使わないで自分で現金化を行う場合、どのように作業を進めていくのかを見ていきましょう。
自分で行うクレジットカード現金化の仕組みや流れをざっくり説明すると、
- 換金率の高そうな商品をクレジットカード決済で購入する。
- 購入した商品をブランド品買取店、金券ショップ、リサイクルショップ、ネットオークションやフリマアプリで売却する。
- 売却代金を受け取る。
という手順になります。
一方、現金化業者に依頼する場合の手順は次のような流れになります。
なお、現金化業者による現金化には、キャッシュバック方式と買取方式があり、最近はキャッシュバック方式が人気となっています。
- 現金化業者に申し込む
- 業者から申し込み内容の確認、本人確認の電話が入る。
- 業者が指定した商品を購入する。
- (キャッシュバック方式の場合)購入特典としてキャッシュバックの現金が振り込まれる。
(買取り方式の場合)商品を業者に発送して買取ってもらい、現金が振り込まれる。 - (キャッシュバック方式の場合)購入した商品を受け取る。
キャッシュバック方式の場合は、商品購入の特典としてキャッシュバックが受けられるものなので、クレジットカード決済後すぐに現金を受け取ることができます。
そのため、自分で現金化する方法だけでなく、買取り方式と比べても、スピーディーに現金化ができます。
業者を使わずに自分でクレジットカード現金化する時のメリット

業者を使わずに自分でクレジットカード現金化する時のメリットは主に次の3点があります。
- 業者に手数料を払わないで済む。
- 個人情報を悪用される恐れが無い。
- 全て自己責任なので換金率に納得できる。
商品を選びクレジットカード決済で購入し、それを売却して現金を入手するまでの過程をすべて自分で行います。
商品選び、購入、売却と手間はかかりますが、業者に手数料を払わないで済むというメリットがあります。
また、悪徳業者の中には高い換金率を提示して集客し、低い換金率で現金化したり、顧客の個人情報を悪用したり、現金を1円も振り込まない詐欺行為を行う業者もいます。
関連ページ:クレジットカード現金化悪徳業者の罠に気を付けろ!業者が儲かる仕組みと詐欺の実態
しかし、クレジットカード現金化をすべて自分で行えば、悪徳業者に関わって損をする心配はありません。
自分で現金化を行うと、品定めに失敗して高く換金できないというような失敗例はありますが、すべて自己責任と考えて行えば割り切ることができます。
業者を使わないで自分でクレジットカード現金化する時のデメリット

クレジットカード現金化を自分で行う方法は、業者を介さずに安全に現金化を行える点が最大のメリットです。
というのも、利用する業者選びを誤ってしまうと、悪徳業者に引っかかり、詐欺被害に遭う可能性があるからです。
しかし残念ながら、メリットだけではありません。
自分でクレジットカード現金化をするときのデメリットもあります。
換金率は一部の業者に敵わない
業者を利用しない分、換金率が業者よりも高くなることを期待する方は多いことでしょう。
業者に支払う手数料がかからないため、その分換金率がよくなるためです。
事実、自分で現金化を行う場合は商品選びに失敗しなければ80~90%の換金率が期待できます。
うまくレア商品を手に入れ現金化すれば、さらにアップすることも可能です。
ただし、品定めに失敗してしまうと、高く売れないどころか買取先が見つからず、現金化に失敗してしまいますので、商品の目利き力が必要になります。
70~80%ほどの換金率を掲げる業者と比較したら、自分で行うほうがより多くの現金を工面することができるでしょう。
しかし最近は、Amazonギフト券の買取業者を中心に90%台の高い還金率を謳う業者が増えてきました。自分で現金化を行ったとしても、これらの業者には敵わないでしょう。
ただし、高い換金率を宣伝する業者の中には、悪徳業者が少なからず混ざっています。
実際に利用してみたら、高い換金率で計算した後でさまざまな理由で手数料を引かれ、結局あまり換金率は高くなかったという例があります。
業者を利用する場合は、業者選びが大切です。
業者選びに自信がない方は、この換金率のわずかな差は「安心料」とみなして自分で現金化することをおすすめします。
ある程度の手間がかかる
これまで紹介したように、現金化を自分で行うには高く売れる商品のリサーチが必要で、商品購入と換金は自分で動かなければなりません。
ブランド品や家電などの旬の商品、人気商品は刻々と変わっていきます。
ネット上でのリサーチや買い物に慣れている方にとってそれは大きな手間ではないかもしれませんが、慣れていない方にとっては非常に面倒なことでしょう。
換金率の高いものを探し、実際に販売されている店に足を運び、あるいはネットショッピングを利用して購入し、それを買取店や金券ショップに売りに行くという作業は思った以上に手間がかかるものです。
忙しく、できれば手間も時間も最小限に抑えたいという方にとっては、それらは大変面倒な作業になることが想像できます。
特に現金化は現金を急いで工面したいときに利用することが多いので、なおさら焦ってしまうのではないでしょうか。
買取業者は換金率を店頭やホームページに出していますので、一番高く買ってくれる業者を調べて持ち込みましょう。
もちろん、商品によってはあまり手間をかけずに自分で現金化することも難しいことではありません。
最近ではAmazonギフト券を利用した現金化などもあり、これを利用すれば店に出向かなくても自宅に居ながらにして自分で現金化することができます。
違法ではないがクレジットカード会社にバレる危険がある

キャッシング枠上限まで借り入れて、さらにショッピング枠上限まで買い物するとクレジットカード会社から警戒されますので注意しましょう。
多額の現金が必要な場合は、高額家電の中から人気商品を選んで購入し換金すれば、一度に多額の現金を手に入れることが可能です。
しかし、そういった高額商品を繰り返し購入するなど、怪しい消費行動をすることで、クレジットカード会社に不正利用を疑われて、カードの利用停止などのペナルティを科せられる可能性もあります。
現金化を疑われた場合に備えて、どこで、何を、なんのために購入したかを答えられるよう準備をしておきましょう。
関連ページ:クレジットカード現金化をカード会社に疑われた時の言い訳と対処法
自分でクレジットカード現金化するときのよくある質問

自分でクレジットカード現金化を行う際に、よくある質問を紹介します。
- 初めてクレジットカード現金化をするのですが、自分で行うのは危険ですか?
- 基本的にはクレジットカードで商品を購入してそれを売却するだけですので、ここで紹介した方法を使い、注意点を守って行えば可能です。
ただ、手間をかけるのが面倒とか、クレジットカードで繰り返し延滞を起こしているなどの事情がある方は、自分で行うより現金化業者を使う方が安全です。 - 急いで現金を手に入れたいのですが、自分で行う現金化では、その日のうちに現金を手に入れることができますか?
- 店舗に出向き商品を購入し、その商品を買取店に持ち込めば、即日現金を手に入れることは可能です。しかし、換金率を高くしようと、商品をネット購入したり、換金率の高い遠方の業者に買取りを依頼したりすると即日現金化は無理になります。
お急ぎの場合はオンラインで手続きができ、即日現金が振り込まれる現金化業者の利用をおすすめします。 - 自分で行う現金化と、現金化業者を使った現金化ではどちらがおすすめですか?
- どちらがおすすめ、お得とは一概に言えません。
悪質業者に関わるのが心配な方、手間がかかっても納得いく現金化をしたいという方には自分で行う現金化をおすすめします。
一方、急に現金が入用になった方、時間が取れず手間がかけられない方には、現金化業者を使った現金化をおすすめします。
自分でクレジットカード現金化はできるけれど 安全かつ多額の取引には優良業者の利用がおすすめ

自分でクレジットカードの現金化を行う具体的な方法やそのメリット・デメリット、注意点について解説しました。
現金化業者の独壇場という印象が強いクレジットカードの現金化ですが、実際に行われている取引は思った以上にシンプルなものです。
どうしても業者を利用したくないという事情がある場合には、自分で現金化を行うことも可能です。
悪徳業者との取引を避けるという点で考えたら、一連の取引を全て自分で行うのはもっとも安全な方法であるといえるでしょう。
しかし自分で行う場合、うまくできたからといって繰り返し現金化をするのは要注意です。
少額の現金化を1,2回するのであれば、自分で行っても問題なくできますが、多額の現金が必要な場合、あるいは毎月現金化が必要な状況にある場合には、業者を使った方が安全に現金化できます。
優良業者を厳選した上で、専門の現金化業者を利用することを検討してみてはいかがでしょうか。
この記事では、クレジットカード現金化業者を使わずに自分でする方法14選!について解説しました。
投稿者プロフィール
























